Извлечём из обеих частей неравенства корень степени ab

Нам требуется доказать, что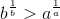  

Исследуем функцию 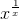  для x > 0.

Судя по графику: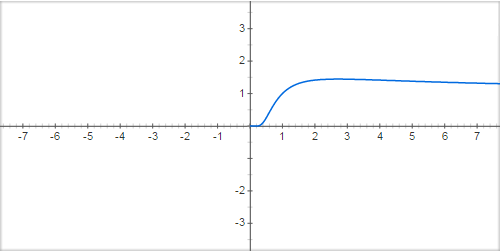

функция возрастает до какой-то точки между 2 и 3, а затем начинает убывать.

Действительно, возьмём производную: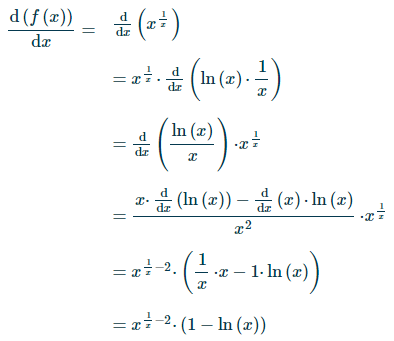

Функция возрастает (производная положительна) до точки, в которой ln x = 1,
т.е. до x = e, а далее убывает (производная отрицательна).

В исходном условии a и b — целые, большие двух числа.
Значит (т.к. функция убывает для x > e), если b < a, то .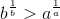

Возводим обе части неравенства в степень ab, получаем требуемое: b^a > a^b